들어가며
이전 포스팅에서는 복잡한 수식이 없이도 Deep learning 의 기본적인 프로세스를 알아보았다.
Sin 함수값을 예측하기 위한 Process로 크게
1. Forward propagation,
2. loss 계산,
3. backward propagation,
4. weight 를 update
를 하는 과정을 거쳤는데 이번 포스팅에서는 세부적으로 알아보고자 한다.
세부 Step 설명
1. Forward propagation
y_pred = a + b * x + c * x**2 + d * x**3 와 같은 수식으로 y 의 예측값인 y_pred를 계산한다.
2. Loss 계산
실제 y 값과 predict 된 값간의 차이로 인해 발생하는 손실을 계산하기 위해 두 값의 차이를 구한 후 이를 제곱하여 합을 취한다. 이렇게 해서 계산된 손실함수는 python code 로 아래와 같이 나타낼 수 있다.
loss = np.square(y_pred - y).sum()
3. Backward propagation
grad_y_pred = 2.0 * (y_pred - y)
grad_a = grad_y_pred.sum()
grad_b = (grad_y_pred * x).sum()
grad_c = (grad_y_pred * x**2).sum()
grad_d = (grad_y_pred * x**3).sum()
grad_y_pred 는 loss 함수에 대해 y_pred 로 미분한 결과이다 (이 때, chain rule 적용됨).
grad_a 는loss 함수를 a 에 대해 미분한 결과로,

이 Loss function 에서 y_pred 를 아래로 치환하여 표현해보자.

이를 a 에 대해 편미분한다.

그러면 chain rule 에 의해 아래와 같이 정리될 수 있다. (이 글에서는 복잡한 수식 없이 이해하는 것을 목표로 하고 있어 세부 산출 과정은 생략 함)
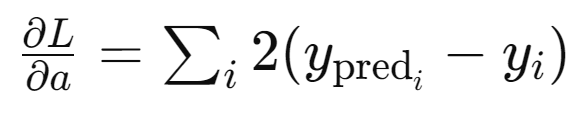
나머지 b, c, d, 에 대해서도 동일한 방식으로 각 b, c, d 로 Loss function 을 편미분하여 Backward propagation 을 실시하면 위에서 보여진 값이 도출된다.
4. weight update
Loss function 의 최저점을 향해 iteration 하는 단계마다 learning rate 를 적용시킨다.
Learning rate 가 크면 weight 가 변하는 정도가 커지기 때문에 학습속도는 빨라지지만 최저점을 지나칠 수 있다는 단점이 있다. 반면 learning rage 가 너무 작으면 weight 가 update 할 때 마다 변하는 정도가 작아져 학습 속도는 느려지지만 안정적으로 converge 할 수 있도록 한다. 이렇게 iteration 을 돌면서 weight 을 learning rate 를 적용시켜 update 시켜서 점진적으로 model 의 성능을 올린다. (즉, Loss function 을 최소화 시킨다)
update 된 weight = update 이전의 weight - learning_rate * gradient_loss 로 간략하게 표현할 수 있다. 여기서 learning rate 를 loss funciton 미분한 값에 곱한 값을 각 a,b,c,d 에서 빼는 이유는 gradient 의 반대방향으로 움직여야 loss function 을 최소화 할 수 있기 때문이다.
